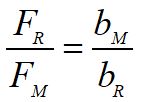ESPERIMENTO DI THOMSON: SCOPERTA DEGLI ELETTRONI

1884 : Edison scopre l’effetto termoelettronico. Un filo metallico incandescente è capace di emettere dei particolari raggi detti "RAGGI CATODICI” perchè emessi dal catodo che è l'elettrodo negativo.

Dal 1880 al 1896: J.J. Thomson studia la natura dei raggi catodici e scopre che sono particelle cariche perché deviate da un campo elettrico. Usando il campo magnetico dimostra che sono cariche negative da come sono deviate.





Nel suo celebre esperimento del 1896 determina il rapporto carica massa di queste particelle che chiama ELETTRONI. Ricordiamo che il rapporto q/m carica-massa identifica in modo univoco la particella. Nel 1905 Millikan determina il valore della carica elementare e ritrova lo stesso rapporto carica massa trovato da Thomson. Quindi si dimostrò che gli elettroni sono i portatori della carica elementare .


ESPERIMENTO:



Thomson usa un tubo (di Crookes) a raggi catodici. Dal catodo viene emesso un fascio di raggi catodici per effetto termoelettronico. I raggi attraversano con una certa velocità il campo elettrico E generato dalle armature di un condensatore. Il raggio viene deviato e la deflessione verticale si può misurare sulla seconda estremità del tubo di Crookes.



Le particelle entrano con velocità v₀ in campo elettrico ortogonale E (condensatore piano).
Subiscono una deflessione d misurabile sullo schermo.




Si ricava il tempo che impiegano per uscire dal condensatore di lunghezza L tenuto conto che la componente del moto nella direzione orizzontale è uniforme: t=L/v₀ . Il tempo trovato si sostituisce nella legge oraria del moto uniformemente accelerato nella direzione verticale ottenendo:



Da questa si può ricavare il rapporto carica massa:



dove y è la deflessione che si può leggere nello schermo dello strumento, E è il campo elettrico applicato.

Manca solo il valore della velocità iniziale v₀ degli elettroni.
Per determinare v₀ si sovrappone al campo elettrico E un campo magnetico B generato da delle bobine percorse da corrente in modo che le linee di forza di B risultino perpendicolari a quelle del campo elettrico e alla direzione del fascio.
Le particelle subiscono così la forza di Lorentz diretta nella stessa direzione del campo E ma in verso opposto.
Si regola la corrente nelle bobine e quindi si regola il campo B fino a quando la deflessione ritorna a zero. La condizione di equilibrio è:

applet : clicca qui

IL MAGNETISMO

Il magnetismo è caratterizzato da due tipi di forza diversa: REPULSIVA e ATTRATTIVA
Ogni magnete è caratterizzato da una estremità detta POLO NORD e da una detta POLO SUD.

Poli magnetici opposti si attirano mentre poli dello stesso tipo si respingono.




Anche il pianeta Terra è un "grande " magnete come scoprì Gilbert nel 1600.
William Gilbert  (1544, 1603)

Per definizione il polo nord del magnete è quello che, se libero di ruotare si orienta verso il polo nord geografico. Quindi il polo sud magnetico si trova in prossimità del polo nord geografico.

Inoltre il polo magnetico terrestre non coincide perfettamente con il polo geografico ma è spostato di circa 11° rispetto all'asse dei rotazione della Terra. La posizione dei poli magnetici terrestri non è sempre stata la stessa. Periodicamente si verifica un'inversione della polarità magnetica come dimostrato dallo studio dei cristalli presenti nelle rocce. (per saperne di più del MAGNETISMO TERRESTRE clicca qui). Il campo magnetico terrestre crea uno schermo protettivo contro il vento solare ed è indispensabile per garantire la vita sul nostro pianeta. Su alcuni pianeti come Marte non è presente nessun campo magnetico.

 

Una manifestazione del magnetismo terrestre sono le aurore boreali generate dalle particelle cariche del vento solare catturate dal campo magnetico più inteso presente ai poli.(clicca qui)



I poli del magnetici sono indivisibili: se spezziamo in due parti il magneti otteniamo due magneti con tutti e due poli magnetici.



Questa è una importante differenza con il campo elettrico .
Quando un magnete risente di una forza diciamo che siamo in presenza di un CAMPO MAGNETICO. Il campo magnetico si può rappresentare con delle linee di forza.

Sperimentalmente si possono evidenziare le linee di forza del campo magnetico ponendo della limatura di ferro su un cartoncino posto sopra un magnete. La limatura si comporta come un insieme di aghi magnetici che in presenza del campo si orientano lungo le linee di forza.

Le linee del campo magnetico sono sempre linee chiuse : escono dal polo Nord ed entrano nel polo Sud .
La magnetizzazione può avvenire per strofinio, per contatto e per induzione.

Si possono magnetizzare oggetti di ferro, acciaio, nichel e loro derivati. Con il riscaldamento a temperatura elevata i corpi magnetizzati perdono il proprio potere magnetico.
Esiste una relazione tra Elettricità e magnetismo ?
I navigatori del 1500 si erano accorti che le bussole impazzivano durante i temporali quando vicino cadevano i fulmini.


applet: simula il campo magnetico generato dal magnete o dalla Terra
CLICCA QUI

Tratto dal FILM "The Core" 2003 

IL BARICENTRO

Il BARICENTRO (centro di massa) di un corpo solido (esteso) è il punto di applicazione della forza peso.

Il corpo si comporta come se tutta la sua massa fosse concentrata nel  baricentro

Se il corpo è omogeneo, il suo baricentro coincide con un suo eventuale centro di simmetria.

Il corpo rimane in equilibrio se si appende con un filo che passa per il baricentro .

Per trovare il baricentro si possono quindi applicare le condizioni di equilibrio:

Per determinare la posizione del baricentro si appende il corpo in un punto e si segna l'asse verticale passante per il punto quando il corpo è in equilibrio. Si ripete il procedimento scegliendo un punto diverso. Il baricentro si trova nell'intersezione degli assi segnati. (vedi video e figura sotto)

Seguono alcuni esperimenti:

Se il punto di sospensione del corpo è sopra al CM l'equilibrio del corpo si dice STABILE perchè se si sposta rispetto alla posizione di equilibrio, il corpo tende a ritornare in quella posizione.

Se il punto di sospensione è sotto CM l'equilibrio del corpo si dice INSTABILE. Infatti basta un piccolo spostamento dalla posizione di equilibrio e il corpo tende a ruotare. L'equilibrio è INDIFFERENTE se il punto di sospensione coincide con il CM.
video di esperimenti sul baricentro della trasmissione Geo Scienza della Rai: CLICCA QUI

LE LEVE

Le leve sono le più semplici macchine meccaniche caratterizzate da  un'asta rigida capace di ruotare intorno ad un punto detto FULCRO.
Sulla leva agiscono due forze:
1) FORZA RESISTENTE FR
2) FORZA MOTRICE FM: forza che bisogna applicare per vincere la forza resistente .

Esempio: (vedi figura sotto)
forza resistente= peso da sollevare
forza motrice= forza esercitata dall'uomo

 bR e bM  sono rispettivamente il braccio della forza resistente e della forza motrice.

Il sistema è in EQUILIBRIO se il momento della forza resistente è uguale e opposto al momento della forza motrice. Quindi:

CONDIZIONE DI EQUILIBRIO DELLA LEVA:

ossia:

LEVA VANTAGGIOSA se  FM < FR  (solo se bM>bR)
LEVA SVATAGGIOSA se FM > FR  (solo se bM<bR)
LEVA INDIFFERENTE se FM = FR (solo se bM=bR)

In base alla posizione del fulcro rispetto al punto di applicazione delle due forze, le leve si possono classificare in:

LEVE DEL PRIMO GENERE : 

Il fulcro si trova tra le due forze

 possono essere vantaggiose, svantaggiose o indifferenti .

esempi: forbici, altalena

LEVE DEL SECONDO GENERE:

La forza resistente si trova tra il fulcro e il punto di applicazione della forza motrice.

sono sempre vantaggiose perchè: bM>bR

esempi: cavatappi, cariola 

LEVE DEL TERZO GENERE

La forza motrice si trova tra il fulcro e la forza resistente.

sono sempre svataggiose perchè bM<bR.

Esempio: pinzetta , avambraccio

 

MOMENTO ANGOLARE DI UN CORPO RIGIDO

Il MOMENTO ANGOLARE di una massa m rispetto a un punto O è il prodotto vettoriale del vettore posizione r e del vettore quantità di moto p:

L'unità di misura è [Kgm²/s]

Il momento angolare è una grandezza analoga alla quantità di moto nel caso rotazionale. Si potrebbe dire che è "la quantità di moto rotazionale". 

 

Per definizione di prodotto vettoriale :

il modulo è :

la direzione è quella perpendicolare al piano contenente i vettori r e p
il verso è quello che si stabilisce con la regola della mano destra:

in particolare è sempre perpendicolare al piano di rotazione e dal suo verso positivo si vede il moto antiorario.

Il momento angolare è massimo quando la massa si muove in direzione perpendicolare al vettore posizione r. Il suo modulo è uguale all'area del parallelogramma con lati r e p.

 

Nel caso di un corpo rigido in rotazione (ad esempio un disco) lo consideriamo composto di tante masse puntiformi che si muovono di moto circolare a distanza ri dal centro di rotazione e con una velocità tangenziale v.
Il momento angolare della singola massa è :

mentre il momento angolare del corpo rigido è la somma dei momenti angolari delle singole masse:

 

Dunque il momento angolare di un corpo rigido che ruota rispetto ad un asse con momento d'inerzia I è dato dall'espressione :

è analoga alla relazione della quantità di moto: p=mv

simulazione di phet
 

video spiega come determinare il verso del momento angolare

Dunque per un corpo rigido in rotazione risulta L=I∙𝛚 e quindi anche: ∆L=I∙∆𝛚 e dividendo per il tempo ∆t si ottiene:

  

e quindi:

Ricordando che per la seconda legge del moto rotazionale:

allora possiamo scrivere la seconda legge in funzione del momento angolare:
II LEGGE DEL MOTO ROTAZIONALE: 

Un momento torcente genera una variazione del momento angolare. E' del tutto analoga alla seconda legge della dinamica espressa nella forma F=∆p/∆t .

CONSERVAZIONE DEL MOMENTO ANGOLARE: Se in particolare il momento totale M applicato al corpo è nullo risulta nulla anche la variazione del vettore momento angolare : 

M=0 → ∆L=0 e allora IL MOMENTO ANGOLARE SI CONSERVA.  

∆L=Lf -Li =0

Li=Lf
Bisogna precisare che se si conserva il momento angolare L allora si conserva la direzione , il verso e il modulo di L. Ricordando che L è per definizione un vettore perpendicolare al piano formato da p e r allora se L si conserva il moto avviene su uno stesso piano.(moto piano)

Nel caso di un corpo rigido in rotazione il momento angolare si mantiene solo se si mantiene invariata la direzione del suo asse di rotazione.

Per un corpo rigido in rotazione intorno ad un certo asse vale anche che:

dove  il primo membro rappresenta il momento angolare iniziale e il secondo quello finale. Se aumenta il momento d'inerzia deve necessariamente diminuire la velocità angolare.

CONDIZIONE PER LA CONSERVAZIONE DEL MOMENTO ANGOLARE:

Abbiamo visto che il momento angolare si conserva solo se la risultante del momento torcente M è nullo.

Ricordando che:

M è nullo solo se Ftot =𝛴F=0 oppure Ftot // r

Quindi il momento angolare di un corpo di massa m si conserva solo se la risultante delle forze esterne applicate al corpo è nulla (SISTEMA ISOLATO) oppure le forze sono di TIPO CENTRALI (forze dirette verso il centro di rotazione).
Un esempio di forza centrale è la forza di gravità che il Sole esercita sulla Terra.

 

 

ESEMPIO: IL Pattinatore