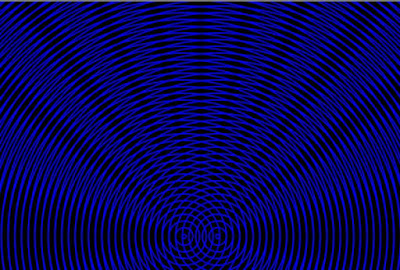
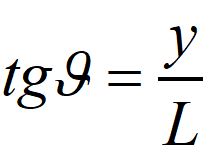Su uno schermo posto ad una distanza L si forma un'immagine d'interferenza caratterizzata da frange luminose (interferenza costruttiva) alternate a frange scure (interferenza distruttiva).
L'esperimento mette in evidenza la natura ondulatoria della luce.
Se lo schermo è lontano e d<<L possiamo considerare paralleli i raggi provenienti dalle due fenditure. Infatti se pensiamo di osservare da una distanza di 5/6 metri le due fenditure tra loro separate da qualche decimo di millimetro vedremo le due fenditure come unica fenditura.
La differenza dei cammini è allora data da :
dove d è la distanza tra le due fenditure .
clicca qui
Il video spiega la condizione di interferenza costruttiva e distruttiva nel caso di due sorgenti circolari coerenti.Nel punto P abbiamo INTERFERENZA COSTRUTTIVA se la differenza dei cammini è multiplo della lunghezza d'onda :
con m= ±1,2,... un numero intero.
Ovviamente al centro dello schermo i raggi arrivano perpendicolari e quindi tra loro in fase. Vi è interferenza costruttiva e si forma il massimo centrale dato da m=0. All'aumentare di m=±1,2,... abbiamo gli altri massimi laterali.
In un punto P dello schermo vi è INTERFERENZA DISTRUTTIVA se la differenza dei percorsi è un multiplo dispari di mezza lunghezza d'onda:
In un punto P dello schermo vi è INTERFERENZA DISTRUTTIVA se la differenza dei percorsi è un multiplo dispari di mezza lunghezza d'onda:
applet simula l'esperimento di Young con diverse frequenze e variando d
Calcoliamo ora la distanza y delle frange luminose e buie dal centro della frangia centrale.
Nell'ipotesi che la distanza L dello schermo sia molto grande rispetto alla distanza d tra le due fenditure l' angolo 𝛳 risulta molto piccolo. Per angoli vicini a zero vale la seguente approssimazione: sen𝛳~𝛳~tg𝛳. Ma la tg𝛳 è data dal rapporto tra il cateto opposto e quello adiacente :
dove y è la distanza del punto P dal centro.
Quindi i punti P con interferenza COSTRUTTIVA si trovano a una distanza dal centro data da :
Possiamo notare che al decrescere della distanza tra le fenditure d oppure all'aumentare della distanza dallo schermo L aumenta la distanza y. Questo corrisponde ad un'immagine d'interferenza allargata con frange più larghe. Lo stesso risultato si ottiene usando luce monocromatica con lunghezza d'onda maggiore (ad esempio luce rossa al posto di luce blu)
In modo analogo si ottiene un'espressione per la distanza delle frange scure (interferenza distruttiva) dal centro:
In particolare misurando la distanza di uno dei massimi dal centro possiamo determinare la lughezza d'onda della sorgente di luce monocromatica:
ATTENZIONE: L'esperimento di Young della doppia fenditura è un fenomeno di interferenza che si verifica insieme ad un fenomeno di diffrazione . Se fosse sono interferenza si dovrebbe vedere una figura composta da un alternarsi di frange chiare e scure della stessa dimensione e con uguale intensità. In realtà non è così.
Il massimo centrale e i massimi secondari della figura di diffrazione appare spezzettato in tante frange di uguale ampiezza e con intensità decrescente. Infatti l'intensità dei massimi della figura d'interferenza è modulata dalla figura di diffrazione secondo il seguente grafico:
clicca qui
Il video spiega l'esperimento di Young
Il video spiega l'esperimento di Young
clicca qui
Esperimento di Young in inglese
Esperimento di Young in inglese