ENERGIA E INTENSITA' DELL'ONDA ELETTROMAGNETICA

Un campo elettrico variabile produce un campo magnetico variabile ad esso perpendicolare e in fase che  a sua volta genera un campo elettrico oscillante e in fase e così via secondo le equazioni di Maxwell . I campi oscillando formano un'onda che si propaga nello spazio. L'onda elettromagnetica è quindi un'onda trasversale costituita da un campo elettrico E e da un campo magnetico B che oscillano su piani tra loro perpendicolari e in fase.  

Possiamo quindi scrivere:

dove k è il numero d'onda e 𝝎 è la pulsazione. Il campo E oscilla nella direzione y mentre il campo B nella direzione dell'asse z mentre l'asse x è la direzione di propagazione. Naturalmente si possono anche esprimere con la funzione coseno. I versi dei vettori E e B sono dati dal vettore di Poynting S così definito:

Il vettore di Poynting fornisce la direzione e il verso della propagazione dell'onda ed è dato dal prodotto vettoriale di E con B. Quindi si applica la regola della mano destra: il pollice è la direzione di propagazione, l'indice del vettore E e il medio del vettore B. Il modulo del vettore di Poynting rappresenta l’intensità istantanea dell’onda elettromagnetica 



Si dimostra che E=cB cioè i moduli dei campi sono tra loro proporzionali e la costante è la velocità della luce c. Da questo si deduce che il valore del campo elettrico è molto più grande del valore del campo magnetico B.

Ricordiamo che :



Le densità di energia del campo elettrico e magnetico sono date dalle formule:



e quindi la densità di energia associata all'onda elettromagnetica si può esprimere con:



dove sostituendo prima E=cB si ottiene:



e poi B=E/c:



e quindi possiamo dedurre che in onda elettromagnetica la densità di energia del campo elettrico E è uguale alla densità del campo B e la densità dell'onda è il doppia di una delle due.

La densità si può esprimere in due modi diversi:


mentre la densità di energia MEDIA si ottiene consideranto i valori efficaci dei due campi:


 
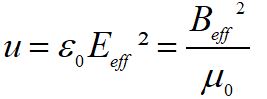
Qual è il significato del valore efficace di E ? Il campo E oscilla tra -E₀ e Eₒ. Vogliamo individuare una grandezza che descriva il campo. Il valore medio è 0. Conviene considerare la media quadratica cioè la media di E² che come funzione è sempre positiva e oscilla tra 0 e E²ₘₐₓ .



Il valore medio del quadrato è dato da:



dalla quale si trova l'espressione di E efficace. In modo analogo quello per B efficace. NB: la media dei valori di E² in un intervallo [0,2𝜋] è (per il teorema della media integrale) da:



dove



L'intensità dell'onda è data dalla potenza su superficie:


dove l'energia è data dalla densità per il volume V:



semplificando risulta :



E quindi sostituendo l'espressione di u:



anche in questo caso per trovare l'intensità media si usano i valori efficaci. L'intensità si può anche esprimere come modulo del VETTORE DI POYNTING che rappresenta il flusso di energia:

la direzione e il verso del vettore di Poyting è quello di propagazione dell'onda.

Il modulo è uguale all'intensita' dell'onda. Basta sostituire E=cB.


Si dimostra che la QUANTITA' DI MOTO associata all'OEM è data da q=E/c dove E è l'energia dell'OEM.

Una radiazione è quindi capace di esercitare una forza e quindi una pressione su una superficie. p=F/A dove F=∆q/∆t



(NB:indico con q la quantità di moto per non confonderla con la pressione)

Calcoliamo la variazione della quantità di moto

∆q=∆E/c=u∙Volume/c=u∙A∙c∙∆t/c=I∙A∙∆t/c (essendo I=u∙c)

Quindi:

F= ∆q/∆t= I∙A/c

p=I/c (PRESSIONE DELLA RADIAZIONE)

lezione dell'MIT sull'argomento