La diffrazione è un fenomeno associato alla propagazione delle onde,
i cui effetti si manifestano quando un’onda incontra un ostacolo o una
fenditura le cui dimensioni sono comparabili o minori rispetto alla
propria lunghezza d’onda.
La diffrazione è la capacità tipica delle onde (e non dei corpuscoli) di propagarsi dietro ostacoli e fenditure di dimensioni comparabili o minori di quelle della lunghezza d'onda.
In accordo col principio di Huygens, dopo che la luce ha attraversato una fenditura, ogni punto della fenditura si comporta come se fosse a sua volta una sorgente di onde circolari e queste onde interagiscono tra loro mediante il fenomeno dell’interferenza creando l'immagine sullo schermo .
Se per la luce valesse l'ipotesi corpuscolare il fascio di luce che attraversa un piccolo foro dovrebbe generare sullo schermo posto davanti una sola frangia di luce. Nel caso dell'ostacolo dovrebbe proiettare un'ombra netta con la stessa forma dell'ostacolo. Così non è. La luce proiettata da una fenditura su uno schermo è caratterizzata da una frangia centrale luminosa e da un alternarsi di frange luminose e scure laterali sempre meno luminose e strette. Questa è una prova a favore dell'ipotesi ondulatoria della luce.
DIFFRAZIONE DA SINGOLA FENDITURA
La figura di diffrazione consiste in una banda centrale larga ed intensa (massimo centrale) affiancata da bande secondarie più strette e meno intense (massimi secondari) e da una serie di bande oscure (minimi). E' proprio la banda centrale molto grande che permette di distinguere la figura di diffrazione dall'interferenza prodotta da due fenditure.
Consideriamo una fessura di larghezza a di dimensioni paragonabili alla lunghezza d’onda 𝞴 della luce. Ogni punto della fenditura genera onde circolari secondarie che si propagano in tutte le direzioni. Se la differenza di cammino delle onde secondarie generate da tutti i punti all’interno della fenditura è pari ad un multiplo della lunghezza d’onda 𝞴 della luce, le onde interferiscono costruttivamente e si ha un massimo nell’intensità di luce sullo schermo. Se la differenza dei cammini è un multiplo dispari di mezza lunghezza si ha un minimo (frangia scura) . (vedi interferenza di onde circolari)
POSIZIONE DELLE FRAGIE SCURE
Dividiamo idealmente la fenditura in due metà di uguale larghezza:
• metà superiore
• metà inferiore
Ogni punto della metà superiore ha un “gemello” nella metà inferiore, alla stessa distanza dal centro, ma speculare.
Consideriamo una coppia di punti simmetrici, uno nella metà superiore e uno nella metà inferiore a distanza a/2 tra loro
In questo caso la differenza di cammino delle onde secondarie "gemelle" (vedi fig. sopra: raggio 5 e 3 oppure del raggio 3 e 1) è uguale a:
se questa differenza di cammino è pari a mezza lunghezza d’onda ho il PRIMO MINIMO dopo il massimo centrale:
e quindi se :
allora si avrà interferenza distruttiva delle due onde (1°minimo)
allora si avrà interferenza distruttiva delle due onde (1°minimo)
Per i minimi successivi, possiamo dividere la fenditura in n parti uguali e richiedere che ogni parte interferisca distruttivamente con la successiva.
Quindi dividiamo la fenditura in n punti da dove partono onde secondarie.
Consideriamo onde secondarie generate da punti della fenditura posti tra loro a una distanza fissata prima a/2, dopo a/4 e così via. Cioè possiamo pensare di dividere la fenditura prima in due parti, poi in quattro e così via. Facciamo questo perché la differenza dei cammini di due raggi uscenti da punti della fenditura posti tra loro ad una data distanza, è sempre la stessa a parità di inclinazione 𝛳 rispetto all'orizzontale .
Consideriamo onde secondarie generate da punti della fenditura posti tra loro a una distanza fissata prima a/2, dopo a/4 e così via. Cioè possiamo pensare di dividere la fenditura prima in due parti, poi in quattro e così via. Facciamo questo perché la differenza dei cammini di due raggi uscenti da punti della fenditura posti tra loro ad una data distanza, è sempre la stessa a parità di inclinazione 𝛳 rispetto all'orizzontale .
Nella figura sopra, sull'asse orizzontale si rappresenta l'intensità della luce che arriva sullo schermo.
Se si applica la condizione precedente a onde secondarie generate da punti della fenditura distanti a/4 si ottiene:
Se si applica la condizione precedente a onde secondarie generate da punti della fenditura distanti a/4 si ottiene:
si ottiene il minimo di secondo ordine.
Infatti il sen𝜃 risulta maggiore del precedente e perciò la posizione è quella successiva rispetto al centro.
In generale posto con m l'ordine del MINIMO posso scrivere:
In generale posto con m l'ordine del MINIMO posso scrivere:
Questa formula indica che più la fenditura è stretta, più grande è l’angolo di diffrazione → il pattern si allarga. Per ipotesi la distanza D dello schermi dalla fenditura è molto grande rispetto alla larghezza della fenditura e quindi: sen𝞋=tg𝞋=y/D
dove y è la DISTANZA del MINIMO dal centro dello schermo e D è la distanza tra la fenditura e lo schermo .Sostituendo sopra si ottiene:
Possiamo determinare la distanza y del minimo di ordine m:
y è direttamente proporzionale alla distanza D dello schermo e inversamente proporzionale all'ampiezza della fenditura. Quindi se aumenta la distanza dello schermo oppure diminuisce l'ampiezza delle denditure allora la figura di diffrazione si allarga e aumentano le frange.
Questa relazione fornisce i valori di y in corrispondenza dei quali la figura di diffrazione ha intensità nulla (frange scure)
Non dice invece nulla sul come varia l’intensità della luce sullo schermo.
Qualitativamente si ha una larga frangia centrale luminosa e molto più intensa, con ai lati un alternarsi di frange chiare molto meno intense.
A parità di fenditura come cambia la figura di diffrazione del laser rosso rispetto a quello verde?
Essendo 𝞴r>𝞴v allora sen𝜃r>sen𝜃v e 𝜃r>𝜃v e quindi le distanze tra le frange sono maggiori per il rosso rispetto al verde. (vedi APPLET2)
A parita di colore della luce e quindi di 𝞴 se diminuisco le dimensioni della fenditura 𝜃 aumenta e quindi la figura di diffrazione si allarga. Ovviamente per ogni coppia di onde secondarie provenienti da punti della fenditura separati dalla stessa distanza a/2 si verifica la stessa condizione ottenuta sopra e sommando su tutte queste coppie di onde secondarie si ottiene il primo minimo nello schermo.
Questa relazione fornisce i valori di y in corrispondenza dei quali la figura di diffrazione ha intensità nulla (frange scure)
Non dice invece nulla sul come varia l’intensità della luce sullo schermo.
Qualitativamente si ha una larga frangia centrale luminosa e molto più intensa, con ai lati un alternarsi di frange chiare molto meno intense.
A parità di fenditura come cambia la figura di diffrazione del laser rosso rispetto a quello verde?
Essendo 𝞴r>𝞴v allora sen𝜃r>sen𝜃v e 𝜃r>𝜃v e quindi le distanze tra le frange sono maggiori per il rosso rispetto al verde. (vedi APPLET2)
A parita di colore della luce e quindi di 𝞴 se diminuisco le dimensioni della fenditura 𝜃 aumenta e quindi la figura di diffrazione si allarga. Ovviamente per ogni coppia di onde secondarie provenienti da punti della fenditura separati dalla stessa distanza a/2 si verifica la stessa condizione ottenuta sopra e sommando su tutte queste coppie di onde secondarie si ottiene il primo minimo nello schermo.
COME VARIA L'INTENSITA'
L'andamento dell'intensità ha la seguente equazione:
L'andamento dell'intensità ha la seguente equazione:
dove 𝛃 è dato dall'espressione:
e quindi:
e il corrispondente grafico è:
Infatti se si disegna il grafico della funzione y=[senx/x]² si ottiene:
esperimento verifica dell'andamento dell'intensità (spettro): clicca qui
clicca qui applet
nell'esperimento si calcola la distanza L tra i due minimi del primo ordine come mostrato in figura e si calcola l'angolo di apertura 𝝱 con sen𝝱=(L/2)/D e poi ricavo la larghezza a della fenditura con a=𝞴/sen𝝱
e il corrispondente grafico è:
Infatti se si disegna il grafico della funzione y=[senx/x]² si ottiene:
esperimento verifica dell'andamento dell'intensità (spettro): clicca qui
clicca qui applet
nell'esperimento si calcola la distanza L tra i due minimi del primo ordine come mostrato in figura e si calcola l'angolo di apertura 𝝱 con sen𝝱=(L/2)/D e poi ricavo la larghezza a della fenditura con a=𝞴/sen𝝱
RETICOLO DI DIFFRAZIONE
Un reticolo di diffrazione è costituito da un gran numero di fenditure sottili poste una vicina all’altra, ugualmente spaziate tra di loro. La distanza tra due fenditure successive si chiama passo del reticolo.
Ad esempio il CD è un reticolo con un passo di 10⁻⁶m.
Se N è il numero di fenditure al cm del reticolo, il passo è d=(1/N) cm.
I raggi che escono da una fenditura si propagano in tutte le direzioni 𝝑.
I raggi provenienti da ogni singola fenditura interferiscono tra loro diversamente in funzione dell'angolo 𝝑. L'osservazione importante è che i raggi paralleli tra loro uscenti dalle singole fenditure hanno la stessa differenza di cammino data da d∙sen𝝑 dove ora d è la distanza tra due fenditure (passo). Per trovare la posizione delle frange di interferenza costruttiva è sufficiente porre questa differenza di cammini uguale a un multiplo di lunghezza d'onda.
Un reticolo di diffrazione è costituito da un gran numero di fenditure sottili poste una vicina all’altra, ugualmente spaziate tra di loro. La distanza tra due fenditure successive si chiama passo del reticolo.
Ad esempio il CD è un reticolo con un passo di 10⁻⁶m.
Se N è il numero di fenditure al cm del reticolo, il passo è d=(1/N) cm.
I raggi che escono da una fenditura si propagano in tutte le direzioni 𝝑.
I raggi provenienti da ogni singola fenditura interferiscono tra loro diversamente in funzione dell'angolo 𝝑. L'osservazione importante è che i raggi paralleli tra loro uscenti dalle singole fenditure hanno la stessa differenza di cammino data da d∙sen𝝑 dove ora d è la distanza tra due fenditure (passo). Per trovare la posizione delle frange di interferenza costruttiva è sufficiente porre questa differenza di cammini uguale a un multiplo di lunghezza d'onda.
I raggi che non sono deviati ( 𝝑=0) interferiscono costruttivamente formando un massimo centrale.
I raggi deviati dell'angolo 𝝑 rispetto all'orizzontale interferiscono costruttivamente se :
d∙sen𝝑=m𝝀 con m=0, ±1, ±2…
d∙sen𝝑=m𝝀 con m=0, ±1, ±2…
Ad esempio il primo massimo si ha per
sen𝝑=𝝀/d
se diminuisce il passo d aumenta 𝝑 e di conseguenza i massimi si allontanano tra loro.Si osserva che la posizione dei massimi dipende anche dalla lunghezza d’onda della luce, e quindi dal colore: il massimo relativo alla luce rossa risulta più spostato rispetto a quello della luce viola. Nel caso del reticolo di diffrazione, le frange appaiono molto più intense e ben definite perché l’interferenza coinvolge un numero elevato di onde provenienti dalle molte fenditure; ciò rende la sovrapposizione costruttiva più selettiva e rafforza notevolmente i massimi.
sen𝝑=𝝀/d
se diminuisce il passo d aumenta 𝝑 e di conseguenza i massimi si allontanano tra loro.Si osserva che la posizione dei massimi dipende anche dalla lunghezza d’onda della luce, e quindi dal colore: il massimo relativo alla luce rossa risulta più spostato rispetto a quello della luce viola. Nel caso del reticolo di diffrazione, le frange appaiono molto più intense e ben definite perché l’interferenza coinvolge un numero elevato di onde provenienti dalle molte fenditure; ciò rende la sovrapposizione costruttiva più selettiva e rafforza notevolmente i massimi.
All’aumentare del numero di fenditure i massimi diventano più intensi e più stretti fino a diventare delle righe ben definite.
Per questo motivo il retico viene utilizzato per separare i colori della luce. Se si usa luce bianca si formeranno delle frange luminose in posizione diversa in base alla lunghezza d'onda del colore. Il risultato è simile a quello che si ottiene con un prisma, tuttavia questi due strumenti sfruttano metodi diversi per separare le componenti cromatiche. Il reticolo sfrutta la diffrazione mentre il prisma usa la rifrazione. Nel caso del reticolo il colore più spostato è il rosso mentre nel prisma il rosso è quello meno deviato.
video lezione politecnico Milano
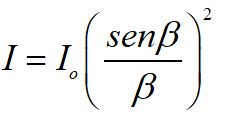
Nessun commento:
Posta un commento