RELATIVITA': CONTRAZIONE DELLE LUNGHEZZE

Consideriamo due sistemi inerziali S e S' con S' che si muove a velocità v rispetto a S. Per facilità pensiamo a S come una stazione ed S' come il treno.

Consideriamo due punti A e B in quiete rispetto al sistema S. Per capire più facilmente la situazione pensiamo a due paletti posti in corrispondenza ai due punti A e B. La distanza Lₒ=AB misurata da S è data da |xA-xB| ed è detta lunghezza propria. 

La LUNGHEZZA PROPRIA è per definizione la distanza misurata tra due punti  in quiete rispetto al sistema di riferimento.
Consideriamo un riferimento T nel sistema S'. Sia:

tA =istante misurato da S con T allineato da A

tB=istante misurato da S con T allineato da B

t'A=istante misurato da S' con T allineato da A

t'B=istante misurato da S' con T allineato da B

S misura il tempo che il punto T impiega a passare dalla posizione A a quella B: 𝛥𝙩=tA-tB

e risulta : Lₒ=v𝛥𝙩

S' misura il tempo che il tempo impiegato da T per passare dalla posizione A a quella B è: 𝛥𝙩'=t'A-t'B. Questo è un TEMPO PROPRIO perché è il tempo tra due eventi che si verificano nello stesso punto rispetto al sistema S'. Per S' la lunghezza è data da L'=v𝛥𝙩'

Ma per la dilatazione dei tempi il tempo misurato da s è dilatato: 𝛥𝙩=𝛾𝛥𝙩' e quindi quello proprio di s' è : 𝛥𝙩'=𝛥𝙩/𝛾.

Sostituendo si ottiene:

L'=v𝛥𝙩/𝛾=Lₒ/𝛾 cioè L'=Lₒ/𝛾

Quindi la lunghezza propria misurata rispetto al sistema in quiete è quella più grande mentre le altre sono contratte di 𝛾≥1.

La contrazione delle lunghezze si verifica solo nella direzione del moto.

ESEMPIO:

Consideriamo questo esempio : L'astronauta Albert parte per la stella Vega distante 25,3 anni luce lasciando il gemello Bart sulla Terra. 

Albert viaggia a una velocità v=0,9c. 
Per Bart che è sulla Terra il viaggio è durato 𝞓t= 25,3c/0,9c=28,1 anni che è un tempo dilatato (non proprio) perchè per lui la partenza e l'arrivo avvengono in luoghi diversi. L'astronave è come il sistema treno S' visto sopra e la Terra e Vega sono i due paletti A e B.   Però per Bart sulla Terra la distanza è propria Lₒ perchè Terra e Vega sono in quiete rispetto a lui. 
Per Albert che è nella navicella, la durata del viaggio è un tempo proprio. Infatti Albert misura la durata del tempo tra  due eventi che avvengono sempre nello stesso punto (sono sempre  in quiete con lui): la partenza e l'arrivo. Dunque per lui il viaggio dura:
𝞓tₒ=𝞓t/𝜸=28,1/2,29=12,3 anni.
Albert e Bart sono d'accordo solo sul valore della velocità relativa v (spazio/tempo). Quindi per Albert è v=L/𝞓tₒ mentre per Bart la distanza è v=Lₒ/𝞓t.
Quindi :
Lₒ/𝞓t=L/𝞓tₒ e risulta che L=Lₒ∙𝞓t/𝞓tₒ=Lₒ/𝜸  . 
L si dice lunghezza contratta perchè 𝜸 è maggiore di 1 e quindi L>L₀.

CON LE TRASFORMAZIONI DI LORENTZ:

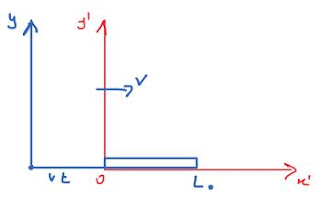
Consideriamo una BARRA di lunghezza L₀ posta lungo la direzione dell'asse delle x e con una estremità in O, in quiete rispetto ad un sistema S' che si muove con velocità relativa v nella direzione dell'asse x rispetto ad un sistema S. 
Ogni osservatore misura la stessa velocità relativa v. 
Dunque per ipotesi le coordinate degli estremi della barra in S' sono:
x'1=0 e x'2=Lo
Quanto vale la lunghezza L misurata da un osservatore posto in S?
L è la distanza delle coordinate degli estremi della barra x1 e x2 prese al tempo t: L=x2-x1
usando le trasformazioni di Lorentz:

Quindi per un osservatore in moto rispetto alla barra la sua lunghezza risulta inferiore rispetto alla lunghezza propria misurata dall'osservatore in quiete rispetto alla barra:

applet: clicca qui

Paradosso del treno di Einstein

lezione app Zanichelli su contrazione della lunghezza

videolezione : contrazione lunghezze