Se v/c è piccolo per passare da un sistema all'altro si usano le trasformazioni Galileiane:
dove il tempo t è per ipotesi lo stesso in tutti i sistemi inerziali (tempo assoluto)Da questo consegue la legge di composizione delle velocità. Se un corpo ha una velocità wx rispetto al sistema S la velocità misurata nel sistema S' è : w'x=wx-v
La luce non si comporta in questo modo. La velocità della luce è la stessa per S e per S' (II POSTULATO della relatività). La differenza si nota quando la velocità relativa dei due sistemi si avvicina a c.
Le trasformazioni Galileiane sono da modificare perché non più valide per sistemi che si muovono con velocità relative prossime a quella della luce.
Ricaviamo le trasformazioni:
Sicuramente è ancora y'=y perché il moto è nella direzione dell'asse x
Posto:
x'=k(x-vt)
x=k(x'+vt') è l'inversa che si deve ottenere per simmetria sostituendo :
v con -v
x con x'
t con t'
per il principio di relatività il k è lo stesso per i due osservatori.
Un raggio di luce che esce dall'origine O al tempo t=t'=0s percorre uno spazio :
x=ct calcolato da S
x'=ct' calcolato da S'
infatti la velocità della luce è la stessa per S e per S'. Sostituendo si ha:
ct'=k(ct-vt)
ct=k(ct'+vt')
se le moltiplico insieme ottengo:
c²tt'=k²tt'(c-v)(c+v)
Semplificato tt' risulta :
detto FATTORE DI LORENTZ.
NB: k =1 per v molto più piccolo della velocità della luce e in questo caso si trasforma nelle trasformazioni Galileiane classiche.
Inoltre si nota che v deve essere sempre minore di 1. Esiste un limite al valore della velocità ed è c.
Determiniamo ora come varia il tempo:
devo ricavare t' in funzione di t. Partiamo dall'equazione : x=k(x'+vt')
x/k=k(x-vt)+vt'
e ricavando t' ottengo:
Quindi le TRASFORMAZIONI dette DI LORENTZ sono:
oppure in forma più compatta:
Sia u la velocità di un corpo misurata in un sistema S. Per ora supponiamo che il corpo si muova nella direzione dell'asse x.
Se u' è la velocità misurata dal sistema S' in moto con velocità v rispetto ad S è data da:
Quindi:
è la legge di composizione delle velocità.
NB: se il corpo che si muove è la luce e u=c allora sostituendo si ottiene che :
e quindi le leggi di trasformazione della velocità sono in accordo con il postulato (la velocità della luce è la stessa per ogni sistema di riferimento e non dipende dalla velocità relativa)
Esempio:
Supponiamo un'astronave si avvicini alla Terra a metà della velocità della luce e spari un missile ad una velocità di 0,750 c. (a) A quale velocità un osservatore legato alla Terra vedrà il missile se viene sparato verso la Terra? (b) Se viene sparato in direzione contraria?
a) posto con S' il sistema del missile e con S il sistema Terra , v=0,5c è la velocità relativa allora se u'=0,75c
b)nel caso b il missile ha velocità u'=-0,75c e sostituendo si ottiene: u=0,4c
ATTENZIONE: per stabilire i segni delle velocità u e u' bisogna capire se vi è avvicinamento o allontanamento del corpo considerato dall'origine del sistema. Il verso della velocità non basta. Infatti vi può essere avvicinamento anche se entrambi procedono nello stesso verso e quello davanti è più lento.
COME CALCOLARE UNA LUNGHEZZA :Per calcolare la lunghezza di un missile che si muove rispetto al sistema S devo determinare le coordinate x1 e x2 delle estremità prese nello stesso istante t1=t2 rispetto al sistema S. Quindi la lunghezza si ottiene con due eventi (x1,t1) e (x2,t1) SIMULTANEI rispetto al sistema S.
Per misurare la lunghezza del missile rispetto ad un sistema di riferimento S' che si muove di moto relativo rispetto a S posso usare la contrazione delle lunghezze se anche rispetto a S' i due eventi sono simultanei altrimenti devo applicare le trasformazioni di Lorentz dei due eventi :
𝛥x'=|x2'-x1'|
Ricordiamo che due eventi simultanei rispetto ad un sistema S non lo sono rispetto a un sistema S'
COME CALCOLARE UN INTERVALLO DI TEMPO : Per calcolare la durata di un fenomeno rispetto ad un sistema S è importante che il fenomeno si verifichi nello STESSO PUNTO x1=x2 : allora
𝛥t=|t2-t1|
La durata del fenomeno rispetto ad un sistema S' che si muove di moto relativo è dato da
𝛥t'=𝛄𝛥t
se anchè rispetto a S' si svolge nello stesso punto (x1'=x2') altrimenti per trovare 𝛥t' bisogna trovare i trasformati dei due eventi con le trasformazioni di Lorentz.


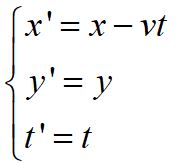










Nessun commento:
Posta un commento