MOMENTO ANGOLARE DI UN CORPO RIGIDO

Il MOMENTO ANGOLARE di una massa m rispetto a un punto O è il prodotto vettoriale del vettore posizione r e del vettore quantità di moto p:

L'unità di misura è [Kgm²/s]

Il momento angolare è una grandezza analoga alla quantità di moto nel caso rotazionale. Si potrebbe dire che è "la quantità di moto rotazionale". 

 

Per definizione di prodotto vettoriale :

il modulo è :

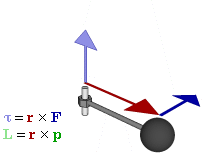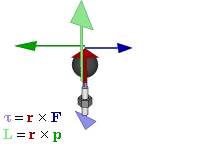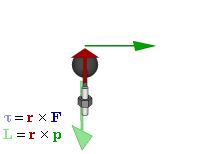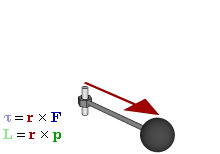
la direzione è quella perpendicolare al piano contenente i vettori r e p
il verso è quello che si stabilisce con la regola della mano destra:

in particolare è sempre perpendicolare al piano di rotazione e dal suo verso positivo si vede il moto antiorario.

Il momento angolare è massimo quando la massa si muove in direzione perpendicolare al vettore posizione r. Il suo modulo è uguale all'area del parallelogramma con lati r e p.

 

Nel caso di un corpo rigido in rotazione (ad esempio un disco) lo consideriamo composto di tante masse puntiformi che si muovono di moto circolare a distanza ri dal centro di rotazione e con una velocità tangenziale v.
Il momento angolare della singola massa è :

mentre il momento angolare del corpo rigido è la somma dei momenti angolari delle singole masse:

 

Dunque il momento angolare di un corpo rigido che ruota rispetto ad un asse con momento d'inerzia I è dato dall'espressione :

è analoga alla relazione della quantità di moto: p=mv

simulazione di phet
 

video spiega come determinare il verso del momento angolare

Dunque per un corpo rigido in rotazione risulta L=I∙𝛚 e quindi anche: ∆L=I∙∆𝛚 e dividendo per il tempo ∆t si ottiene:

  

e quindi:

Ricordando che per la seconda legge del moto rotazionale:

allora possiamo scrivere la seconda legge in funzione del momento angolare:
II LEGGE DEL MOTO ROTAZIONALE: 

Un momento torcente genera una variazione del momento angolare. E' del tutto analoga alla seconda legge della dinamica espressa nella forma F=∆p/∆t .

CONSERVAZIONE DEL MOMENTO ANGOLARE: Se in particolare il momento totale M applicato al corpo è nullo risulta nulla anche la variazione del vettore momento angolare : 

M=0 → ∆L=0 e allora IL MOMENTO ANGOLARE SI CONSERVA.  

∆L=Lf -Li =0

Li=Lf
Bisogna precisare che se si conserva il momento angolare L allora si conserva la direzione , il verso e il modulo di L. Ricordando che L è per definizione un vettore perpendicolare al piano formato da p e r allora se L si conserva il moto avviene su uno stesso piano.(moto piano)

Nel caso di un corpo rigido in rotazione il momento angolare si mantiene solo se si mantiene invariata la direzione del suo asse di rotazione.

Per un corpo rigido in rotazione intorno ad un certo asse vale anche che:

dove  il primo membro rappresenta il momento angolare iniziale e il secondo quello finale. Se aumenta il momento d'inerzia deve necessariamente diminuire la velocità angolare.

CONDIZIONE PER LA CONSERVAZIONE DEL MOMENTO ANGOLARE:

Abbiamo visto che il momento angolare si conserva solo se la risultante del momento torcente M è nullo.

Ricordando che:

M è nullo solo se Ftot =𝛴F=0 oppure Ftot // r

Quindi il momento angolare di un corpo di massa m si conserva solo se la risultante delle forze esterne applicate al corpo è nulla (SISTEMA ISOLATO) oppure le forze sono di TIPO CENTRALI (forze dirette verso il centro di rotazione).
Un esempio di forza centrale è la forza di gravità che il Sole esercita sulla Terra.

 

 

ESEMPIO: IL Pattinatore