Uno dei principi fondamentali della fisica è la legge di conservazione della quantità di moto : In un sistema isolato (somma delle forze esterne =0) la quantità di moto totale di un sistema di corpi si mantiene costante.
Se m ed M sono le masse del sistema e vi,ui sono le loro velocità iniziali e vf, uf sono quelle finali, risulta:
mvi+Mui=mvf+Muf
Per il principio di relatività Galileiano la conservazione della quantità di moto vale in tutti i sistemi inerziali.
Infatti passando ad un sistema inerziale S' che si muove di velocità relativa Vt, secondo la legge di composizione delle velocità cambiano le velocità dei due corpi prima e dopo:
m(vi -Vt)+M(ui-Vt)=m(vf-Vt)+M(uf-Vt)
e questa è vera perché è equivalente alla precedente.
Per velocità molto elevate bisogna usare le trasformazioni di Lorentz ed è evidente che non vale più se non si cambia la definizione della quantità di moto .
Perché rimanga valido tale principio bisogna modificare la definizione della quantità di moto p che in relatività diventa:
dove m0 è detta MASSA A RIPOSO del corpo ed è la massa misurata nel sistema IN QUIETE con il corpo .
per valori di v<0,4c la definizione coincide con quella classica.
In realtà, la stessa espressione potrebbe anche essere riscritta in una forma del tutto equivalente ma concettualmente diversa senza dover definire una massa dipendente dalla velocità.
Basta considerare la velocità v=∆r/∆t₀ che appare nella definizione della quantità di moto come il rapporto fra lo spostamento ∆r di un corpo in un dato riferimento S (lunghezza propria) e l'intervallo di tempo proprio ∆t₀ misurato nel sistema riferimento del corpo (tempo proprio). Quindi per la dilatazione dei tempi ∆t=𝛾∆t₀ e ∆t₀=∆t/𝛾
Osservazione : Per comprendere la situazione basta a pensare al corpo come al sistema S' treno e al sistema S come la stazione. Il tempo misurato rispetto al sistema del treno è proprio perchè compreso tra due eventi che si verificano nella stessa posizione.
Sostituendo nella definizione di quantità di moto:
Con tale definizione di quantità di moto di un corpo vale il PRINCIPIO DI CONSERVAZIONE DELLA QUANTITA' DI MOTO anche per velocità relativistiche.
Nel caso classico, l'equazione del moto di un corpo è data dalla II legge di Newton. Anche in relatività vale la seconda legge: F=dp/dt
dove p è la quantità di moto relativistica.
Allo stesso modo, perchè continui a valere la LEGGE DI CONSERVAZIONE DELL'ENERGIA:
Risulta la quantità di moto di un corpo di massa m che si muove con velocità v rispetto a un sistema S è data da : p=𝛾∙mv
Nel caso classico, l'equazione del moto di un corpo è data dalla II legge di Newton. Anche in relatività vale la seconda legge: F=dp/dt
dove p è la quantità di moto relativistica.
Allo stesso modo, perchè continui a valere la LEGGE DI CONSERVAZIONE DELL'ENERGIA:
Per il momento non prendiamo in considerazione l'energia gravitazionale. In fisica classica un corpo con massa m e velocità v rispetto a un sistema S ha solo energia cinetica data da E=1/2mv². Se il corpo è fermo per v=0 la sua energia totale è nulla. Ricordiamo che la legge di conservazione dell'energia rimane vera anche in relatività: l'energia totale si conserva.
Per questo motivo si deve ridefinire l'energia totale di un corpo di massa m e velocità v in questo modo :
ossia:
e nel caso v=0m/s (sistema SOLIDALE con il corpo e corpo FERMO rispetto al sistema di riferimento) l'energia non è nulla come in fisica classica ma è data da:
Quindi un corpo possiede energia per il solo fatto di possedere una massa. La massa è quindi una forma di energia potenziale. ( EQUIVALENZA TRA MASSA E ENERGIA)
NB: l'energia a riposo ha un valore molto grande di energia . Ad esempio 1kg di massa possiede un'energia E=1kgc²=9∙10¹⁶J
Questa è l'energia è paragonabile con l'energia consumata dall'Italia in un anno.
Nella produzione di energia nucleare tramite fissione una piccola diminuzione di massa è trasformata in energia:
∆E= ∆m∙c²
L'energia cinetica è invece data dalla differenza tra l'energia totale e quella a riposo:
Se v=c l'energia cinetica diverge a infinito. Dunque un corpo può raggiungere la velocità della luce solo se gli viene fornita un'energia cinetica infinita. Quindi è IMPOSSIBILE per un corpo dotato di massa raggiungere la velocità della luce che rimane la massima velocità possibile.
LIMITE DI VELOCITA' DEL COSMO = c
Questo si spiega anche in questo modo:
Un corpo aumentando la sua velocità aumenta anche la sua massa relativistica e quindi la sua inerzia. Per aumentare ulteriormente la sua velocità necessiterebbe di una sempre maggiore energia.
per velocità <0,4c l'energia relativistica si può approssimare a :
In fisica relativistica la massa non si conserva ma continua a conservarsi l'energia. Infatti una certa quantità di massa può essere persa perché trasformata in energia:
Segue una video lezione di dinamica relativistica:
ossia:
e nel caso v=0m/s (sistema SOLIDALE con il corpo e corpo FERMO rispetto al sistema di riferimento) l'energia non è nulla come in fisica classica ma è data da:
E0=mc² (detta ENERGIA A RIPOSO)
NB: l'energia a riposo ha un valore molto grande di energia . Ad esempio 1kg di massa possiede un'energia E=1kgc²=9∙10¹⁶J
Questa è l'energia è paragonabile con l'energia consumata dall'Italia in un anno.
Nella produzione di energia nucleare tramite fissione una piccola diminuzione di massa è trasformata in energia:
∆E= ∆m∙c²
L'energia cinetica è invece data dalla differenza tra l'energia totale e quella a riposo:
Se v=c l'energia cinetica diverge a infinito. Dunque un corpo può raggiungere la velocità della luce solo se gli viene fornita un'energia cinetica infinita. Quindi è IMPOSSIBILE per un corpo dotato di massa raggiungere la velocità della luce che rimane la massima velocità possibile.
LIMITE DI VELOCITA' DEL COSMO = c
Questo si spiega anche in questo modo:
Un corpo aumentando la sua velocità aumenta anche la sua massa relativistica e quindi la sua inerzia. Per aumentare ulteriormente la sua velocità necessiterebbe di una sempre maggiore energia.
per velocità <0,4c l'energia relativistica si può approssimare a :
In fisica relativistica la massa non si conserva ma continua a conservarsi l'energia. Infatti una certa quantità di massa può essere persa perché trasformata in energia:
UNITA' DI MISURA PER L'ENERGIA e MASSA IN FISICA NUCLEARE:
Per l'energia si usa l'elettrovolt: 1eV=1,6∙10⁻¹⁹J
per la massa si usa 1eV/c²=1,6∙10⁻¹⁹J/3∙10⁸=1,78∙10⁻³⁶ Kg
Segue una video lezione di dinamica relativistica:
Segue una semplice, chiara discussione sull'equivalenza MASSA - ENERGIA di una nota trasmissione radio:
Altro invariante relativistico è dato da: E²-p²c²
dove m (massa a riposo) e c sono invarianti. Quindi:
Altro invariante relativistico è dato da: E²-p²c²
Infatti dal calcolo risulta:
e da questa si ricava un'espressione dell'energia in funzione della quantità di moto:
In particolare possiamo calcolare l'energia del fotone (massa a riposo nulla):



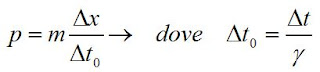











Nessun commento:
Posta un commento