Un moto si dice oscillatorio se un corpo si muove avanti e dietro intorno ad un punto di equilibrio. Il moto armonico è un particolare moto oscillatorio che si può definire come segue:
Il moto armonico è il moto della proiezione sull’asse x (oppure asse y) di un punto P che si muove di moto circolare uniforme di raggio R.
il punto blu sull'asse x e il punto rosso sull'asse y si muovono di moto armonico
Una massa applicata ad una molla e un pendolo che oscilla sono esempi di moti armonici.
L'AMPIEZZA A del moto è la massima distanza dal centro e coincide con il raggio R della traiettoria circolare.
Il PERIODO del moto è il tempo necessario per un'oscillazione completa. La frequenza è il numero di oscillazione nell'unità di tempo.
La velocità angolare del moto circolare è chiamata PULSAZIONE del moto armonico e si indica ancora con 𝝎 :
Per definizione la velocità angolare è 𝝎=𝞓𝛂/𝞓t. Quindi lo spostamento angolare è : 𝛂=𝝎t .
Il vettore posizione del moto armonico è la proiezione ortogonale sull'asse x del vettore posizione del moto circolare uniforme.
Quindi applicando cateto=ipotenusa x coseno dell'angolo adiacente:
x=Rcos𝛂 dove R è il raggio che coincide con l'ampiezza A del moto armonico
Possiamo scrivere la LEGGE ORARIA del moto armonico nella forma: x(t)=A⋅cos(𝝎t)
Il vettore posizione del moto armonico è la proiezione ortogonale sull'asse x del vettore posizione del moto circolare uniforme.
Quindi applicando cateto=ipotenusa x coseno dell'angolo adiacente:
x=Rcos𝛂 dove R è il raggio che coincide con l'ampiezza A del moto armonico
Possiamo scrivere la LEGGE ORARIA del moto armonico nella forma: x(t)=A⋅cos(𝝎t)
Ovviamente considerando la proiezione sull'asse y si otteneva in modo equivalente : y(t)=A⋅cos(𝝎t+𝛗)
E' facile mostrare che in generare la legge oraria è del tipo: x(t)=A⋅cos(𝝎t+𝛗) dove 𝛗 si chiama fase e il suo valore dipende dalla posizione di partenza (per t=0) del moto armonico. Se parte dall'estremità 𝛗=0 , se parte dal centro 𝛗=𝛑/2. 𝛗 è un angolo in radianti che corrisponde alla posizione angolare del raggio nel moto circolare associato.
Allo stesso modo il vettore velocità del moto armonico è la proiezione sull'asse x (o y) del vettore velocità tangenziale del moto circolare. Si deduce che la velocità v del moto armonico è nulla negli estremi ed è massima pari a vₚ=𝝎⋅R nel centro.
dove vₚ=𝝎⋅R=𝝎⋅A
Allora la legge della velocità del moto armonico è data da:
v(t)=-𝝎⋅A⋅sen(𝝎t)
v(t)=-𝝎⋅A⋅sen(𝝎t)
il segno - è dovuto al verso del vettore che è sempre rivolto verso il centro O.
Allo stesso modo l'accelerazione
del moto armonico è la proiezione del vettore accelerazione centripeta
sull'asse x .
E' quindi nulla al centro ed è massima di valore 𝝎²R agli estremi.
Si deduce che dove la velocità è NULLA, l'accelerazione è MASSIMA e viceversa.
E' quindi nulla al centro ed è massima di valore 𝝎²R agli estremi.
Si deduce che dove la velocità è NULLA, l'accelerazione è MASSIMA e viceversa.
Ricordando che l'accelerazione centripeta è data da :
a=v²/R=𝝎²∙R
l'equazione dell'accelerazione del moto armonico è data da:
a=v²/R=𝝎²∙R
l'equazione dell'accelerazione del moto armonico è data da:
a(t)=- 𝝎²A∙cos(𝝎∙t)
essendo: x(t)=A⋅cos(𝝎t)
RISULTA:
a(t)= - 𝝎²∙x(t)
Quindi il moto di un punto è armonico se e solo se l'accelerazione in valore assoluto è direttamente proporzionale alla posizione x(t). Questa condizione si può assumere come definizione del moto armonico. La costante è 𝝎² cioè il quadrato della pulsazione. Quindi per dimostrare che un certo moto è armonico e sufficiente mostrare che la sua accelerazione è direttamente proporzionale alla posizione. Inoltre dall'equazione a(t)=- 𝝎²A∙cos(𝝎∙t) possiamo dedurre che l'accelerazione è massima negli estremi dove la velocità è nulla ed è nulla al centro dove la velocità è massima. Il valore massimo dell'accelerazione si ottiene infatti quando il vettore accelerazione centripeta è verticale e la sua proiezione sull'asse y coincide con l'intero vettore.
LEGGE ORARIA
L'ampiezza è il massimo valore di y mentre il periodo è l'ampiezza dell'intervallo tra due picchi consecutivi.
Se il punto parte da una posizione diversa cioè se nell'istante iniziale l'angolo è 𝞅 allora l'equazione diventa più in GENERALE: x(t)=A∙cos(𝝎t+𝞅)
𝞅 si dice FASE INIZIALE.
Esempio: Se il moto parte dall'estremità sinistra verso destra allora la fase è 180° e cos (𝝎t+180°)=-cos(𝝎t). Se invece parte dal punto O e si muove verso sinistra allora la fase
𝞅=90°. cos(𝝎t+90°)=sen(𝝎t)
𝞅=90°. cos(𝝎t+90°)=sen(𝝎t)
Quindi il moto armonico si può esprimere anche con la funzione seno se parte dal centro o si considera la proiezione sull'asse y. La legge oraria in funzione del seno è: y=A∙sen(𝝎t+𝞅)
LETTURA DEI GRAFICI:
Dal grafico x-t possiamo dedurre l'ampiezza del moto e il suo periodo.
Il moto del SISTEMA MASSA MOLLA (detto oscillatore armonico) è un esempio di moto armonico.
il video della pssc mostra come ricavare il grafico del moto armonico. (ITA)
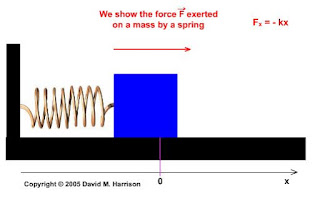
per dimostrare che è un moto armonico devo mostrare che l'accelerazione è proporzionale allo spostamento a=-kx .
Nell'oscillatore armonico la forza che agisce è la forza elastica F=-k∙x dove k è la costante elastica della molla. Applicando la II legge della dinamica F=m∙a si ottiene l'equivalenza ma=-kx e quindi a=-(k/m)∙x .
L'accelerazione è dunque proporzionale allo spostamento.(cvd)
L'accelerazione è dunque proporzionale allo spostamento.(cvd)
Inoltre la costante di proporzionalità è: 𝝎²=(k/m)
Quindi la pulsazione di un oscillatore armonico dipende solo dalla costante elastica della molla e dalla massa applicata.
Per aumentare il periodo (e quindi rallentare il moto) bisogna aumentare la massa oppure diminuire la costante della molla.
ANALISI DELL'ENERGIA:
Nel moto armonico dell'oscillatore massa- molla l'energia si conserva. Nell'estremità l'energia totale è data solo dall'energia potenziale : E=U=1/2 k A²
Infatti v=0 e quindi l'energia cinetica è nulla.
Al centro avviene il contrario. L'energia potenziale è nulla mentre l'energia cinetica è massima data da E=1/2 m v²=(1/2)m∙(𝝎∙A)².
Per la legge di conservazione dell'energia si deduce che:
e quindi 𝝎²=k/m che è vera.
Per dimostrare che l'energia totale si mantiene costante si esegue il seguente calcolo:
Esercizio:
Osserva il seguente grafico del moto armonico di un corpo.
Dal grafico ricava il valore del periodo T, dell'ampiezza A,la fase e la legge oraria del moto.Ricordando che la velocità in un istante t è uguale alla pendenza della retta tangente nel punto (t,y), ricavare i valori della velocità per t=0s, t=0,5s, t=1s, t=1,5s e t=2s . Disegnare il grafico della velocità.
[y=2cos(𝜋t)]
Esercizio:
Esercizio:
ripetere l'esercizio precedente con il seguente grafico:
Nel seguente video della pssc si studia il moto di un oscillatore armonico mostrando che ha un moto armonico semplice.
Altro esempio di moto armonico semplice è quello del pendolo:
ogni pendolo ha una lunghezza diversa e quindi un periodo e una frequenza diversa di oscillazione. L'effetto che si ottiene è quello mostrato nel video
Altro esempio di moto armonico semplice è quello del pendolo:
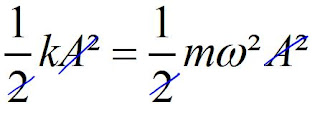
Nessun commento:
Posta un commento