La videolezione (ITA) spiega il problema del corpo nero.
Il problema nasce dallo studio di un semplice fenomeno: la luce emessa da corpi riscaldati.
Ad esempio un ferro rovente inizialmente emette prevalentemente nell'infrarosso e la sua luce è rossa . Poi, quando la temperatura sale ulteriormente, il suo colore diventa prima giallo e poi bianco - azzurro.
Ogni corpo ad una temperatura T emette una radiazione elettromagnetica che risulta visibile solo per temperature sufficientemente elevate.
Si notò anche che la luce emessa da corpi riscaldati alla stessa temperatura risulta del medesimo colore che quindi non dipende dalla natura del materiale.
La fisica classica spiegava il fenomeno dicendo che ogni corpo è formato da atomi che sono liberi di oscillare come delle molle intorno al loro punto di equilibrio. La temperatura definisce la temperatura come una misura della velocità media di oscillazione degli atomi. Maggiore è la temperatura, maggiore è la velocità di oscillazione degli atomi (agitazione termica).
Per la teoria dell'elettromagnetismo ogni carica oscillate è sorgente di onde elettromagnetiche. Quindi un corpo scaldato emette radiazioni perché le cariche presenti nell'atomo sono in oscillazione.
La questione diventò ovviamente di grande interesse con l'invenzione dalla lampadina ad incandescenza di Edison.
Lo studio del colore e della luce generata da un corpo caldo era strettamente legato al miglioramento dell'efficienza della lampadina. Si cercava una relazione tra il colore della luce e la sua temperatura. Nel 1881 nella conferenza delle unità di misura di Parigi si tentò senza successo di definire un campione di luminosità per mancanza di conoscenze teoriche sulla luce. L'industriale tedesco Siemens finanziò questa ricerca con l'intenzione di introdurre nel mercato una lampadina innovativa da un punto di vista energetico.
Il fisico tedesco Kirchoff definì un modello ideale di corpo (detto CORPO NERO) capace di assorbire ed emettere tutte frequenze della radiazione SENZA RIFLETTERE nessuna radiazione.
Infatti un corpo che non riflette radiazione è nero perché il colore di un oggetto è dato dalla componente della radiazione riflessa.
Un corpo illuminato con luce bianca appare rosso perchè assorbe tutte le componenti cromatiche escluso il rosso che viene riflesso.
Se invece il corpo appare nero è perchè assorbe tutte le componenti cromatiche ma non è escluso che possa riflettere qualche frequenza fuori dal visibile (ad esempio infrarossi) continuando ad apparire alla nostra vista nero.
qualunque corpo con una certa temperatura è sorgente di radiazione infrarossa visibile con telecamere per la visione notturna
Il CORPO NERO pensato da Kirchoff è un corpo che è "nero" per tutte le frequenze dalle onde radio ai raggi gamma.Un CORPO NERO è quindi un corpo che assorbe ed emette tutte frequenze delle radiazioni elettromagnetiche senza riflettere nulla e che è in grado di emettere radiazione cromatica qualora sia riscaldato a temperature diverse.
Bisogna fare molta attenzione a distinguere il colore di un corpo illuminato dato dalla luce riflessa, dal colore del corpo nero dato dalla radiazione emessa dallo stesso corpo. Quello che interessa il fenomeno è la "luce" emessa.
Ma come è fatto un corpo nero?
In genere, è rappresentato come un oggetto cavo che comunica con l'esterno tramite un foro. Quando le radiazioni entrano nella cavità, si riflettono sulle pareti interne restando intrappolate e, infine, sono assorbite dal corpo. Di conseguenza il corpo nero è sempre in equilibrio termico perchè emette quanto assorbe. Se, ad esempio, guardiamo dall'esterno le finestre di un appartamento queste ci appaiano nere anche se dentro c'è luce perché la quantità di luce che entra dalla finestra è maggiore di quella che esce.
Possiamo considerare come corpo nero anche il Sole, una qualunque stella oppure il filo incandescente della lampadina. In generale lo è ogni corpo ad una certa temperatura T che è in equilibrio termodinamico.
Per radiazione del corpo nero si intende solo la radiazione emessa in virtù della sua temperatura.
E' un corpo
perfettamente assorbente. E' in grado di assorbire tutte le radiazioni
elettromagnetiche in entrata ( assorbitore ideale o corpo emissivo
ideale ) ed emettere radiazioni su tutte le lunghezze d'onda (
emettitore ideale ).
In genere, è rappr
E' un corpo
perfettamente assorbente. E' in grado di assorbire tutte le radiazioni
elettromagnetiche in entrata ( assorbitore ideale o corpo emissivo
ideale ) ed emettere radiazioni su tutte le lunghezze d'onda (
emettitore ideale ).
In genere, è rappr
E' un corpo
perfettamente assorbente. E' in grado di assorbire tutte le radiazioni
elettromagnetiche in entrata ( assorbitore ideale o corpo emissivo
ideale ) ed emettere radiazioni su tutte le lunghezze d'onda (
emettitore ideale ).
In genere, è rappr
E' un corpo
perfettamente assorbente. E' in grado di assorbire tutte le radiazioni
elettromagnetiche in entrata ( assorbitore ideale o corpo emissivo
ideale ) ed emettere radiazioni su tutte le lunghezze d'onda (
emettitore ideale ).
E' un corpo
perfettamente assorbente. E' in grado di assorbire tutte le radiazioni
elettromagnetiche in entrata ( assorbitore ideale o corpo emissivo
ideale ) ed emettere radiazioni su tutte le lunghezze d'onda (
emettitore ideale ).
In genere, è rappr
Del corpo nero si voleva studiare il suo spettro cioè il grafico dell'intensità della radiazione emessa in funzione della frequenza (o della lunghezza d'onda)
Dove nasce il problema del corpo nero?
L'interpretazione classica del corpo nero prevedeva una emissione infinita di energia .
Infatti l'energia dell'onda elettromagnetica in fisica classica è associata alla sola ampiezza dell'onda e non alla frequenza. Il corpo nero deve, per definizione, emettere su tutte le frequenze che sono ovviamente infinite. Anche se su ogni frequenza è emessa una radiazione di bassa energia (piccola ampiezza) la somma di infinite quantità finite risulterebbe comunque infinita.
Ovviamente pensare ad una energia infinita andava contro la legge di conservazione dell'energia.
Inoltre la distribuzione dello spettro di frequenze prevista era diversa da quella effettivamente osservata.
Qual'era allora l'errore di interpretazione?
SPETTRO DEL CORPO NERO
Come già detto la distribuzione dell'energia della radiazione del corpo nero sulle diverse frequenze, prevista dalla fisica classica risultava sostanzialmente diversa da quella osservata.
Prima di tutto dobbiamo chiarire che cos'è lo spettro di emissione di un corpo.
Ogni corpo ad una temperatura T emette sempre radiazione elettromagnetica .
Ad esempio una lampadina ad incandescenza irradia infrarossi e luce visibile.
La radiazione emessa da un corpo si può descrivere con lo spettro del corpo (grafico Intensità - Frequenza oppure Intensità-lunghezza d'onda) che indica l'intensità della radiazione e quindi la quantità di energia al secondo su unità di superficie relativa alla frequenza emessa.
esempio di spettro di una lampadina led e della luce solare. La curva mostra l'energia emessa per ogni lunghezza d'onda. Il led emette buona parte della sua energia sulla lunghezza d'onda del verde. Non emette energia sull'ultravioletto che è invece emesso dal sole come si vede dal secondo spettro.
Lo spettro del corpo nero, ricavato dalle leggi della fisica classica era una curva crescente al crescere della frequenza. Il problema dell'infinita energia risultante dalla teoria venne chiamato problema della "catastrofe ultravioletta".
Lo spettro, ricavato poi sperimentalmente alla fine del 1800, dimostrava un andamento sostanzialmente diverso con una forma caratteristica a campana. Il problema si poteva risolvere ricavando una legge matematica che descriveva correttamente l'andamento della curva a campana e capire qual'era l'errore nella curva ricavata dalla teoria.
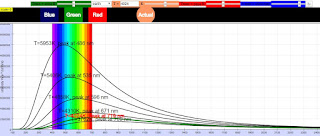
Lo spettro del corpo nero è uno spettro CONTINUO (cioè assume valori su tutte gli infiniti valori reali delle frequenze) con la tipica forma a "campana" dove il PICCO DI EMISSIONE è la lunghezza d'onda a cui corrisponde la massima emissione (massima INTENSITÀ) della radiazione emessa.Un primo importante risultato venne ottenuto nel 1899 dal giovane fisico austriaco W.Wien. Wien capì che lo spettro del corpo nero DIPENDE SOLO dalla temperatura T del corpo e non dipende dalla sua natura.
Il picco di emissione è invece quello che caratterizza il colore di cui appare il corpo se scaldato a quella temperatura. Aumentando la temperatura il picco di emissione si sposta verso una lunghezza d'onda più piccola.
Wien scoprì che il prodotto della lunghezza d'onda corrispondente al picco di emissione per la temperatura assoluta del corpo è sempre una costante. La LEGGE detta DELLO SPOSTAMENTO DI WIEN si scrive con l'espressione :
La lunghezza d'onda di picco è inversamente proporzionale alla temperatura assoluta del corpo.
La costante è :
Tramite questa legge è possibile determinare la lunghezza d'onda di picco di qualunque corpo nero ad una certa temperatura.
In modo equivalente la frequenza è direttamente proporzionale alla temperatura con costante 5,88·10¹º s⁻¹K⁻¹:

Nello spettro con intensità -frequenza lo spostamento è verso destra a frequenze maggiori. (vedi sotto)
Viceversa dal colore emesso dal corpo nero (cioè dalla frequenza corrispondente) si può dedurre la sua temperatura. Ad esempio dal colore del Sole si può dedurre il picco di emissione (la frequenza del giallo/rosso) e quindi la sua temperatura di circa 5800K.
Alla fine del 1800 era nota anche la LEGGE DI STEFAN - BOLTZMANN ricavata con metodi termodinamici:
NB: P è uguale all'area sottesa dal grafico dello spettro a campana essendo l'integrale della funzione.
Alla fine dell'800 era quindi noto il grafico che caratterizzava lo spettro del corpo nero ma tutti i tentativi di spiegare teoricamente la curva dello spettro del corpo nero ricavando l'espressione analitica della funzione I(𝝀,T) fallirono miseramente.
spettro in funzione della frequenza
spettro in funzione della lunghezza d'onda
Infatti per frequenze maggiori la funzione continuava a crescere in modo esponenziale (DIVERGENTE). Quindi secondo tale modello l'energia irradiata dal corpo nero diventava infinita per alte frequenze e ciò andava contro la legge di conservazione dell'energia. Questo problema passò alla storia con il nome di CATASTROFE ULTRAVIOLETTA.
Nel 1900 Max Planck trovò una funzione matematica che si accordava perfettamente con i dati sperimentali ma alla quale non riusciva inizialmente a dare una spiegazione teorica.

Successivamente propose una SOLUZIONE rivoluzionaria partendo dall'ipotesi che l'energia fosse emessa o assorbita in modo DISCRETO (quantizzato) secondo pacchetti elementari di energia (e quindi non in modo continuo come si era sempre pensato!!).
La quantità minima di energia (QUANTO DI ENERGIA) è direttamente proporzionale alla frequenza e valeva:

dove h è detta COSTANTE DI PLANCK

La costante è molto piccola e questo è il motivo della difficoltà di evidenziare la natura discreta dell'energia nel caso macroscopico.
Inoltre l'energia scambiata ad una frequenza maggiore avviene con quanti di energia più gradi di quelli alle piccole frequenze. Questo evita la "catastrofe ultravioletta" perché l'energia emessa dal corpo nero è finita e alle frequenze più alte è più difficile che avvenga l'emissione di energia.
Seguono delle video lezioni in italiano sull'argomento:
SIMULAZIONE APPLET
Max Planck e l'inizio della quantistica
per approfondire in inglese
























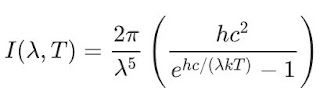
Nessun commento:
Posta un commento