Per questo motivo ad ogni punto P del campo si può associare un valore UP di energia in modo tale che il lavoro fatto dalle forze del campo per spostare una carica da A a B si può esprimere come differenza:
L=UA-UB
L'energia potenziale in un punto P dipende dalla carica posta in P ed è definita a meno di una costante che dipende da dove poniamo uguale a zero U. (è analogo al caso gravitazionale)
Il POTENZIALE ELETTRICO in un punto P del campo è l'energia potenziale su unità di carica e questo valore non dipende più dalla carica posta nel punto P ma solo dalla posizione.
L'unità di misura è il Volt : 1V=1J/1C
In questo modo il lavoro svolto dalle forze del campo per spostare la carica q dal punto A al punto B si esprime con la formula:
Una linea (o superficie) si dice EQUIPOTENZIALE se è formata da tutti punti con lo stesso potenziale. Il lavoro per spostare una carica su una linea equiponteziale è zero e infatti le linee equipontenziali sono perpendicolari in tutti i loro punti al campo elettrico .
Una carica positiva tende a muoversi dal potenziale maggiore a quello minore (questo è quindi il verso del campo elettrico). Quella negativa in verso opposto.
La superficie esterna di un corpo conduttore è sempre una superficie equipotenziale e il campo elettrico è sempre perpendicolare alla superficie ed è sempre nullo nella parte interna.
Anche per il potenziale in un punto vale il principio di SOVRAPPOSIZIONE:
Il potenziale
elettrico totale in un punto P dovuto a due o più cariche è uguale alla somma algebrica dei potenziali
dovuti a ogni singola carica separatamente.
CAMPO RADIALE
Nel caso del campo radiale generato da una carica puntiforme Q , l'energia potenziale in un punto P a distanza r dove è posta una carica q è data da :
Allora l'energia potenziale è posta uguale a zero all'infinito e U(r) è equivalente al lavoro fatto contro le forze del campo per portare una carica dall'infinito fino ad una distanza r dalla carica Q che genera il campo.
Infatti la carica q è respinta da Q e quindi bisogna compiere un lavoro per avvicinarla fino ad una distanza r e questo lavoro si accumula sotto forma di energia potenziale U. Usando l'analogia con il campo gravitazionale è simile a quando si compie un lavoro per sollevare una massa m da terra. La situazione è anche simile a quella di una molla che viene compressa e che accumula energia potenziale elastica.
L'energia potenziale elettrica di un sistema di cariche è uguale al lavoro per portare le cariche dall'infinito alla loro posizione. Per portare la prima carica Q il lavoro è nullo, per portare la seconda q ad una distanza r dalla prima il lavoro è dato da :
per portare una terza carica q' si deve compiere un lavoro dovuto alla singola presenta della carica Q e della carica q
In totale l'energia del sistema è la somma di questi lavori:
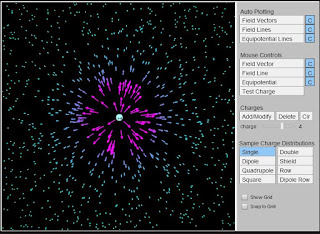
APPLET: simula campo elettrico e potenziale CLICCA QUI
applet : simula il moto delle cariche in un campo rappresentato dalle linee equipotenziali come dislivelli gravitazionali CLICCA QUI
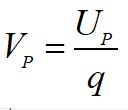
Nessun commento:
Posta un commento