martedì 17 dicembre 2013
giovedì 10 ottobre 2013
GIOCO ON LINE:CONVERSIONI DELLE UNITA' DI MISURA : AREA E VOLUME
CONVERSIONI DELLE UNITA' DI MISURA :
AREA E VOLUME
Sposta con il mouse i corpi con il valore del volume equivalente e permetti all'omino di avanzare.
ESEMPIO DI GRANDEZZE INVERSAMENTE PROPORZIONALI (APPLET)
Hai due recipienti con superficie di base diversa. Devi calcolare l'altezza che il fluido raggiunge quando lo travasi nell'altro recipiente.
Si tratta di RELAZIONE DI PROPORZIONALITA' INVERSA tra l'altezza h del fluido e la superficie di base S:
Sh=costante
il prodotto delle due grandezze è costante (è la quantità di fluido)
CHI VUOL ESSERE MILIONARIO: GIOCO CON LE UNITA' DI MISURA
CHI VUOL ESSERE MILIONARIO
Funziona come il classico quiz televisivo solo che le domande sono tutte sulle unità di misura.
Buon divertimento!
CLICCA QUI
CLICCA QUI
GIOCHI CON LE EQUIVALENZE DELLE UNITA' DI MISURA DELLA LUNGHEZZA
CLICCA QUI
Il gioco consiste nel appendere al gancio il valore equivalente per permettere all'omino di avanzare.
Il gioco consiste nel appendere al gancio il valore equivalente per permettere all'omino di avanzare.
Il gioco consiste nel associare a due a due le misure di lunghezze equivalenti. Quando termini passi ad un livello successivo. Vediamo quanti punti riesci a fare.
G
M
T
La funzione vocale è limitata a 200 caratteri
| Opzioni : Cronologia : Opinioni : Donate | Chiudere |
sabato 5 ottobre 2013
giovedì 26 settembre 2013
GIOCO CON CONVERSIONI DELLE UNITA' DI MISURA
Il gioco consiste nel scrivere la conversione delle unità di misura proposte e premere invio. Se la risposta è corretta un omino salirà nella giostra panoramica. CLICCA QUI
mercoledì 25 settembre 2013
SIMULATORI DEL CAMPO ELETTRICO
Mostra le linee di campo generate da due cariche aventi il segno opposto o con lo stesso segno. Si può variare il rapporto tra le due cariche. CLICCA QUI
ALTRO SIMULATORE DI CAMPO ELETTRICO CLICCA QUI
ALTRO SIMULATORE DI CAMPO ELETTRICO CLICCA QUI
martedì 17 settembre 2013
LEZIONE: LE GRANDEZZE FISICHE E LA MISURA
LA MISURA E LE GRANDEZZE FISICHE: misure dirette e indirette, unità di misura , campioni, Sistema Internazionale , analisi dimensionale
giovedì 5 settembre 2013
STUDIO DEGLI URTI
Un sistema di due corpi che in un piano si urtano si può considerare in SISTEMA ISOLATO
Nello studio degli urti tra due corpi si possono distinguere due casi:
URTI ELASTICI: se si conserva la quantità di moto e l'energia
URTI ANELASTICI: se si conserva solo la quantità di moto. Parte dell'energia cinetica è dissipata sotto forma di deformazione dei corpi , in calore o in energia sonora. In particolare si chiama urto TOTALMENTE ANELASTICO quando i due corpi proseguono uniti con la stessa velocità dopo l'urto.

Con questo programma puoi studiare gli urti tra 2 corpi
Consideriamo il seguente problema : Date le masse m e M dei due corpi, e le loro velocità iniziali v e V , determinare le loro velocità u e U dopo l'urto.
Il caso più semplice è quello dell'urto TOTALMENTE ANELASTICO:
PRIMA DELL'URTO: p=MV+mv
DOPO L'URTO: p=(M+m)u
essendo u la velocità finale dei due corpi
Per la legge di conservazione della quantità di moto: MV+mv=(M+m)u
si ricava : u=(MV+mv)/(M+m)
Un esempio di urto totalmente anelastico è quello del pendolo balistico. Per misurale la velocità del proiettile di un'arma si spara un colpo con velocità v₀ sul pendolo. Il pendolo di massa M con il proiettile di massa m conficcato dentro si muove con velocità v' sollevandosi di h che si misura. Per la legge di conservazione della quantità di moto la velocità del proiettile è data
v₀= (M+m)v'/m
v₀= (M+m)v'/m
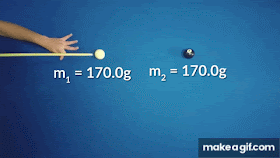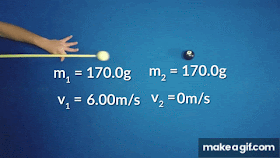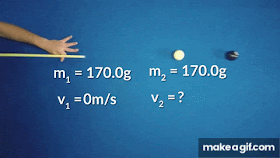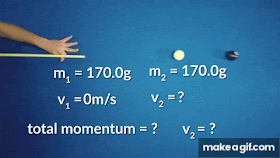
URTO ELASTICO UNIDIMENSIONALE:
Consideriamo ora l'urto elastico tra due masse m₁ e m₂
e con opportuni passaggi si ottiene:
ATTENZIONE : se i due corpi si vengono incontro scontrandosi la velocità iniziale del corpo di massa m₂ è da intendersi negativa.
ATTENZIONE : se i due corpi si vengono incontro scontrandosi la velocità iniziale del corpo di massa m₂ è da intendersi negativa.
Nel caso particolare del BERSAGLIO FERMO si ottiene v₂i =0
cioè il proiettile e bersaglio si scambiano la velocità . Il primo si ferma e parte il secondo con la stessa velocità del primo. Tipico esempio di ciò lo si può osservare nel pendolo di Newton:
ALLENAMENTO CON LE PERCENTUALI
ALLENAMENTO CON LE PERCENTUALI
COME SI GIOCA: è come il memory solo che bisogna associare alla frazione l'equivalente percentuale. Ad esempio a 1/10 il 10%
ESERCITAZIONE DI MISURA
Sai eseguire della misure di lunghezze con la stecca da disegno . Prova ad esercitarti con questo gioco.
Sciegliere se eseguire misure intere, decimali o frazionarie. Scrivere la lettura eseguita nella casella di testo e cliccare su CHECK
Sciegliere se eseguire misure intere, decimali o frazionarie. Scrivere la lettura eseguita nella casella di testo e cliccare su CHECK
mercoledì 31 luglio 2013
DECOUVERTE : IL DISCO DI BENHAM
IL DISCO DI BENHAM
Una conseguenza della persistenza delle immagini è di causare la comparsa di colori su un disco in bianco e nero (con opportuna distribuzione del bianco e del nero) che ruota molto velocemente.
Una conseguenza della persistenza delle immagini è di causare la comparsa di colori su un disco in bianco e nero (con opportuna distribuzione del bianco e del nero) che ruota molto velocemente.
LA CURVA BACHISTOCRONA: LA CICLOIDE
LA CICLOIDE
video girato AL MUSEO DE'COUVERTE DI PARIGI
Un problema di cui la cicloide fornisce la soluzione è la DETERMINAZIONE DELLA BRACHISTOCRONA , ovvero la curva di discesa più rapida. A porsi per primo la domanda fù Johann Bernulli nel 1697;il suo quesito recitava più o meno così: “Dati due punti Ae B su un piano verticale in un campo gravitazionale uniforme, trovae la curva tra essi sulla quale un punto materiale, vincolato a scorervi senza attrito vada da quello più alto a quello più in basso nel minor tempo possibile”.
Istintivamente si potrebbe
pensare che la distanza più breve tra due punti è il segmento di retta, ma non
è così perché conviene puntando il più possibile verso il basso per
acquistarela massima velocitàiniziale. Galileo aveva già affrontato molti anni
prima ed aveva creduto di risolverlo indicando come traettoria ottimale l’arco
di cerchi. In realtà, la traettoria ottimale è la cicloide che per questo è
detta anche curva brachistocrona, cioè del tempo più breve.
La soluzione matematica di
questo problema costituì uno dei primi successi del calcolo differenziale che
verso la fine del 1600 era stato inventato indipendentementeda Newton e
Leibniz.
Nel video si può notare che le palline poste sul profilo di cicloide arrivano alla base nello stesso momento anche se partono da altezze diverse. Questa è un'altra proprietà della curva.
giovedì 27 giugno 2013
QUESITO IDROSTATICO
Riempi un bicchiere di acqua e mettilo sulla bilancia. Ora inserisci un dito dentro l'acqua senza toccare il fondo del bicchiere o le sue pareti. Secondo te il peso aumenta, diminuisce o rimane uguale?
Per scoprirlo guarda il video realizzato dagli alunni del "Liceo Leopardi Majorana" di Pordenone.
ESPERIMENTO : DIAVOLETTO DI CARTESIO (FLUIDI)
TITOLO: Il diavoletto di Cartesio
MATERIALI:
-
Recipiente di plastica trasparente (Altezza 30 cm
circa, diametro 6 cm circa)
-
Membrana in plastica (materiale simile a quello dei
palloncini)
-
Oggetto in vetro con la faccia inferiore convessa (in
modo tale da avere uno spazio
interno vuoto a contatto con l’esterno nella
parte inferiore); in questa esecuzione è stato utilizzato un oggetto a forma di
diavoletto.
PROCEDIMENTO:
Si riempie il recipiente in plastica con acqua (fino ad
arrivare quasi all’orlo) e vi si immerge il diavoletto (deve essere pesante a
sufficienza in modo tale che affondi completamente fino ad una profondità
intermedia tra il fondo e l’orlo.
Si chiude l’estremità del recipiente stirando la membrana in
plastica in maniera che sia ben tesa e fissata.
OSSERVAZIONI:
- Esercitando una pressione sulla membrana di
plastica, ad esempio premendo con il dito sulla stessa, l’oggetto in vetro,
situato inizialmente ad un’altezza intermedia, tende a scendere verso il basso
del recipiente (sebbene non vi sia stato alcun contatto diretto tra il dito e
l’oggetto stesso)
SPIEGAZIONE:
In condizioni normali, all’interno dell’oggetto in vetro,
nella sua parte concava, si viene a creare una bolla d’aria, ovvero una sacca
che possiede densità inferiore rispetto all’acqua e impedisce al diavoletto di affondare completamente.
Quando una pressione dall’alto viene esercitata sul liquido, esso – per il
principio di Pascal – essa si trasmette su ogni parte di esso e lo comprime.
Viene compressa, quindi, anche la bolla d’aria (l’aria, in quanto gas, può
essere facilmente compressa) che diminuisce di volume; lo spazio lasciato
libero da essa viene occupato dal liquido. La densità del diavoletto, allora, aumenta ed esso tende ad affondare.
Il seguente video mostra l'esperimento realizzato dagli alunni del liceo "Leopardi Majorana " di Pordenone nell'anno scolastico 2013-2014
lunedì 25 marzo 2013
ESPERIMENTI SUL PRINCIPIO DI ARCHIMEDE
Liceo Leopardi Majorana di Pordenone
Progetto Archimede
2012 - 2013
1) BAROSCOPIO
2) RELAZIONE TRA LA SPINTA D’ARCHIMEDE E LA PORZIONE DI VOLUME IMMERSO
sabato 2 febbraio 2013
GIOCO CON LE UNITA' DI MISURA (PREFISSI)

Il gioco consiste nel riordinare in ordine crescente le unità di misura con prefisso della lunghezza o della massa ... per costruire il bruco.
















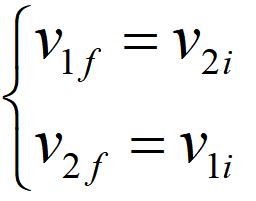



 g
g
